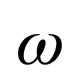Запутанное квантовое превосходство
Эпиграф: Видишь, какой я путник… то есть нет, путаник © Страшила
Если вы освоились с представлением кубита в виде вектора, можно поговорить о квантовой запутанности.
Запутанность квантовых частиц проявляется в том, что их измерения оказываются скореллированы, как бы далеко частицы не находились друг от друга. Например, если у одной частицы мы измерили спин, и он оказался «вверх», то другая как бы мгновенно об этом узнаёт, и её спин становится «вниз».
Важно понимать, что у запутанных частиц коррелируют не внутренние состояния, а именно результаты измерения. Строго говоря, состояние отдельной запутанной частицы вообще отсутствует, во всяком случае в виде вектора. Есть лишь состояние системы двух частиц как целого, и вот его можно представить в виде вектора, но уже в другом, общем базисе. И оно неразложимо на состояния отдельных частиц.
Запутаем два кубита так, чтобы они давали разные значения при измерении в базисе |0⟩ и |1⟩. Получится такой вектор: |ψ⟩ = 1/√2*|0⟩|1⟩ + 1/√2*|1⟩|0⟩. Это суперпозиция двух состояний с равной вероятностью 1/2. В первом состоянии один кубит имеет значение 0, другой — 1, во втором — наоборот.
Чему равно состояние каждого кубита в этой суперпозиции? На первый взгляд кажется, что для обоих кубитов это просто суперпозиция состояний 0 и 1: |φ⟩ = 1/√2*|0⟩ + 1/√2*|1⟩ = |p⟩. Но это иллюзия. Если бы это было так, то оба кубита давали бы всегда один и тот же результат |p⟩ при измерении в базисе |p⟩ и |m⟩. А что будет на самом деле?
Если выразить векторы |0⟩ и |1⟩ через |p⟩ и |m⟩ и подставить в формулу общего состояния, получим: |ψ⟩ = 1/√2*|p⟩|p⟩ — 1/√2*|m⟩|m⟩. То есть они действительно будут всегда давать один и тот же результат, но случайный — либо два |p⟩, либо два |m⟩, а вовсе не только |p⟩. При разложении по любому базису запутанные частицы всегда остаются запутанными.
Так что в системе запутанных частиц бессмысленно искать состояние каждой отдельной частицы. Можно лишь говорить о вероятности получения определённого состояния после измерения либо об исходном состоянии всей системы.
У незапутанных частиц вектор состояния системы можно представить в виде произведения состояний отдельных частиц, у запутанных — нельзя. Это в некотором роде и есть определение запутанности.
Из этого вытекает интересное следствие. Два незапутанных кубита (даже если каждый отдельно в суперпозиции) можно моделировать просто двумя двумерными векторами. А вот если мы хотим моделировать любые их состояния, включая запутанные, нам уже двух двумерных векторов будет недостаточно, придётся заменить их на один четырёхмерный вектор. Для трёх кубитов — один восьмимерный и т. д.
Кроме того, что это не масштабируемо (добавление одного кубита ведёт к перестройке всей модели), так сама размерность вектора растёт экспоненциально. Для 50 кубитов нам потребуется уже петабайт памяти, чтобы просто сохранить одно состояние системы (если каждый коэффициент занимает один байт). А без запутывания мы могли бы обойтись всего ста байтами. Как говорится, почувствуйте разницу.
Так что именно запутанность (а не просто суперпозиция) — один из факторов превосходства квантовых компьютеров над классическими. Доказано, что если в квантовом алгоритме количество запутанных частиц не превышает логарифм от всего числа частиц, то такой алгоритм имеет эффективный классический аналог.
Но что интересно, запутанность — необходимый, но недостаточный критерий квантового превосходства. Другими двумя критериями являются сложность квантовых гейтов и разветвлённость схемы их соединения. Если хотя бы одно из трёх условий не выполняется, квантовый алгоритм можно с тем же успехом заменить классическим.
Возможно, есть и другие условия, которые пока не обнаружены. Поэтому-то так сложно ответить на вопрос, что именно даёт квантовому компьютеру ту мощь, которую ему приписывают. Это ещё открытая область исследований.