Спин электрона и неравенства Белла
Спин электрона — это векторная величина. Он характеризуется направлением, как, например, скорость. Как и скорость, его можно разложить на составляющие по некоторому базису (системе координат). Только в отличие от скорости длина вектора спина всегда равна одному и тому же значению, условной единице.
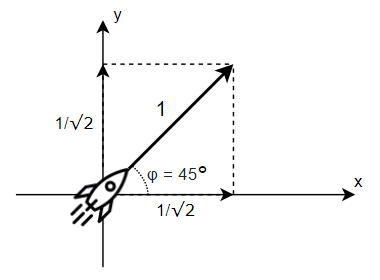
Например, если ракета летит под углом 45° к земле со скоростью 1 км/с, мы можем измерить её горизонтальную и вертикальную скорости, обе получатся равны 1/√2 км/с. В принципе, то же можно проделать и со спином. Например, пусть спин электрона направлен так же под углом 45°. Мы можем измерить его в горизонтальном направлении. Он получится равен 1/√2. Стоп, нет! Это невозможно, спин не может быть дробным.
Что же тогда мы получим при измерении? Оказывается, для разных электронов мы получим разный результат. Для одних измеренный спин будет направлен вправо (засчитаем его как +1), для других — влево (засчитаем его как -1). Но что интересно — если мы возьмём среднее арифметическое по результатам измерений многих электронов, мы как раз и получим примерно 1/√2.
То же самое будет для других направлений. Если ракета летит вертикально вверх, её горизонтальная скорость равна нулю. Если спин измеряемых электронов направлен вертикально вверх, то их измеренный горизонтальный спин в среднем будет тоже равен нулю, хотя для каждого отдельного электрона мы получим +1 или -1 с вероятностью 50%.
Возникает вопрос, «знает» ли электрон заранее свой спин по каждому направлению или он генерируется случайным образом в момент измерения? В первом случае результат измерения детерминирован неким внутренним состоянием электрона, которое нам неизвестно, но тем не менее присутствует внутри. Во втором случае никакого такого внутреннего состояния нет, а результат измерения истинно случаен.
В этом и заключался спор Эйнштейна и Бора. Эйнштейн выступал за первый вариант, Бор — за второй. И никто из них не надеялся, что спор можно будет разрешить экспериментально. В самом деле, как можно проверить, есть ли у электрона внутреннее ненаблюдаемое состояние? Но вот пришёл Белл и объяснил, что можно. К сожалению, ни Эйнштейн, ни Бор до этого не дожили.
Интересно, что для понимания неравенств Белла не требуется знания сложной математики. Достаточно элементарной теории множеств. Но почему-то в интернете почти нет доступных объяснений. Попробуем этот пробел исправить.
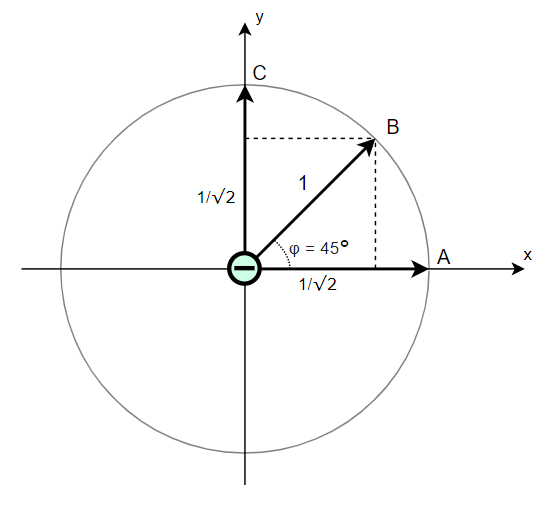
Сначала предположим, что прав Эйнштейн. Спин по каждому направлению уже заранее содержится внутри электрона. При измерении мы просто его узнаём.
Возьмём пачку электронов и измерим спин каждого из них по двум перпендикулярным направлениям A и C. Предсказания квантовой теории нам говорят, что измерения совпадут в 50% случаев. То есть из всех электронов, у которых внутри скрыт спин A+, половина внутри должны иметь спин C+, а вторая половина C-. И наоборот — из C+ электронов половина должна быть A+, а половина A-. Заметим, что это возможно, только когда количество A+ и C+ электронов одинаково.
Такую конфигурацию легко представить при помощи кругов Эйлера (на самом деле диаграмм Венна), Вот, например, для случая, когда A+ и C+ электронов по 8 штук:
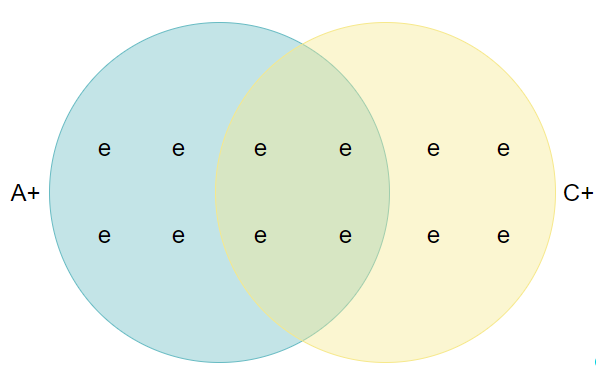
Теперь изменим угол и будем измерять спин по направлениям A и B, под 45° друг к другу. Если у нас линейная зависимость вероятности от угла, то мы получим 75% совпадений. Заметим, что снова количество A+ и B+ электронов должно совпадать, чтобы процент работал в обе стороны.
Теперь возьмём направления B и C. Поскольку между ними у нас тоже 45°, то и по ним мы должны получить 75% совпадений. И количество B+ и C+ тоже должно совпадать. В кругах Эйлера это будет выглядеть так:
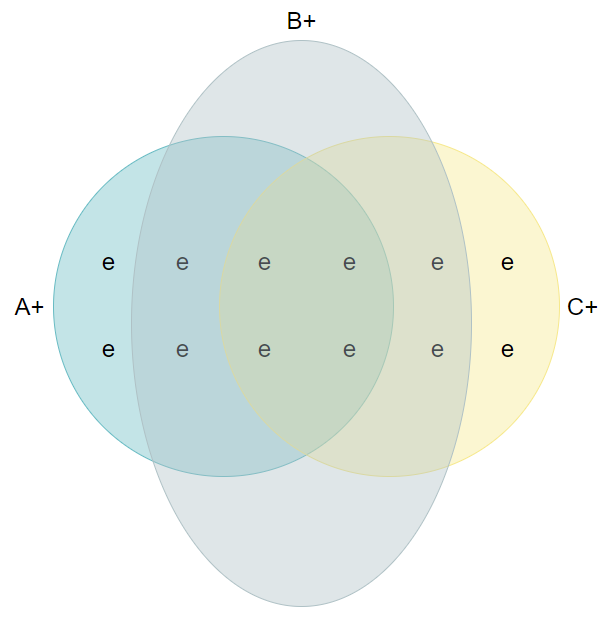
Теперь важный момент. Если вдруг зависимость от угла у нас нелинейная, то вместо 75% мы получим какой-нибудь другой процент. Но он не может превышать 75%. Это видно по картинке. Если пересечение A+ и C+ составляет половину от B+, то B+ может дополнительно содержать только ещё четверть от A+ и четверть от C+, никак не больше.
То есть 75% — это максимально допустимый процент совпадений под 45° в модели Эйнштейна, когда спин по всем направлениям задан заранее. Для большего процента вы не сможете подобрать скрытые параметры электронов в выборке так, чтобы выполнялись все указанные выше соотношения. Такого множества просто не существует.
Ну и что вы думаете? Квантовая механика требует, чтобы этот процент был больше 75%, а именно в районе 85%.
Это легко посчитать. Помните, мы говорили, что среднее арифметическое спина, измеренного под 45° к исходному, должно равняться 1/√2? Подставим это число в формулу матожидания и найдём вероятность p:
p * (+1) + (1 — p) * (-1) = 1/√2
2p — 1 = 1/√2
p = (1 + 1/√2) / 2 = 0.8535...
Зависимость от угла тут не линейная, а косинусная, т. к. 1/√2 в данном случае — это не что иное как cos 45°.
Так что вы не сможете подобрать такое множество электронов со скрытыми спинами, чтобы в нём A+ электроны пересекались с B+ на 85%, B+ с C+ — тоже на 85%, но при этом A+ с C+ — на 50%. У вас обязательно где-нибудь не сойдётся.
Что говорит о том, что теория скрытых параметров неверна, электрон не содержит внутри информацию о своих спинах по всем направлениям, а при измерении получается по-настоящему случайный результат. И прав был Бор, а не Эйнштейн.
Тут внимательный читатель наверное уже извёлся, доказывая мне, что так не работает. Ведь если мы измеряем один электрон по разным направлениям, то ведь каждое измерение влияет на состояние электрона и может изменять его скрытые параметры. А мы почему-то предполагаем, что они остаются неизменными. Так что наше доказательство — не доказательство.
Совершенно верно, в таком виде — не доказательство. Поэтому вместо последовательных измерений одного электрона производят параллельные измерения на паре спутанных электронов, спин которых всегда противоположен друг другу. Например, один электрон измеряют по направлению A, другой — по направлению B и т. д.
Для каждой пары спутанных электронов выбирают случайную пару направлений — AB, AC или BC, а затем усредняют цифры по каждой паре направлений. Электроны предварительно разносятся на приличное расстояние, а измерения делаются одновременно, чтобы убедиться, что один электрон не успел передать другому информацию со скоростью света.
Проведённые многочисленные эксперименты все подтвердили правильность предсказаний квантовой теории, поэтому либо электроны не содержат скрытых параметров, либо они общаются быстрее скорости света. Вторая опция (сверхсветовое влияние), кстати, тоже допустима, и в частности она используется в теории волны-пилота. Так что не надо забывать, что Белл отменил скрытые параметры не совсем, а только при отсутствии сверхсветового взаимодействия.
P. S. Идею объяснения теоремы Белла я взял из этого видео:
Только у них там всё объясняется на примере поляризации света, а я адаптировал для спина электронов.