Суперпозиция и базис
Как известно, квантовый бит (кубит) в отличие от обычного бита может находиться не только в состоянии 0 или 1, но и в суперпозиции этих двух состоянии, то есть как бы содержать оба этих значения в некоторой пропорции. При измерении же происходит схлопывание суперпозиции к одному из базовых состояний 0 или 1.
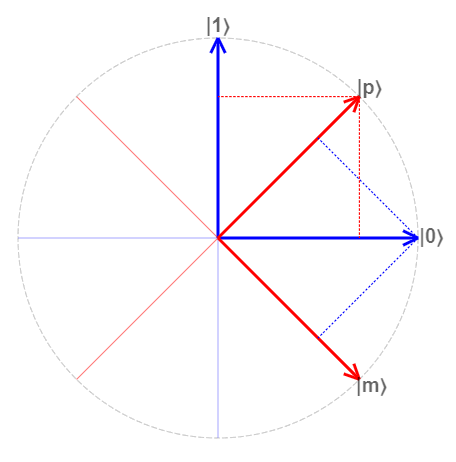
Состояния кубита удобно представлять в виде векторов. Тогда всякое состояние можно записать в виде линейной комбинации базовых векторов |0⟩ и |1⟩ с соответствующими коэффициентами: |φ⟩ = x*|0⟩ + y*|1⟩. Коэффициенты определяют вероятность соответствующего результата измерения, а именно: вероятность получить ноль будет равна x2, а единицу — соответственно y2.
Поскольку вероятность получить хоть какой—то результат равна единице, то x2 + y2 = 1. А это у нас не что иное, как уравнение единичной окружности. Поэтому состояние кубита всегда есть единичный вектор, указывающий на точку единичной окружности.
Например, состояние p на картинке будет записано так: |p⟩ = 1/√2*|0⟩ + 1/√2*|1⟩ ≈ 0.71*|0⟩ + 0.71*|1⟩, и вероятность получить каждый исход в нём будет одинакова и равна 1/2. Это пример суперпозиции, как и любая другая точка на окружности за исключением двух базовых векторов |0⟩ и |1⟩.
Суперпозицию иногда понимают так, что кубит находится сразу в двух состояниях одновременно и параллельно. Однако, вектор |p⟩ ничем принципиально не отличается от вектора |0⟩. Состояние p — это такое же чистое и однозначное состояние, как и состояние 0. Никакого распараллеливания в нём нет.
Например, если 0 кодируется как спин вверх, а 1 — как спин вниз, то p — это просто спин вбок (например, вправо). Это вовсе не означает спина вверх и вниз одновременно. Эффект суперпозиции проявляется лишь при измерении. Если частицы со спином вправо измерять по вертикали, то мы будем получать спины вверх и вниз с равной вероятностью.
Но мы ведь можем измерять их и по горизонтали. Тогда мы всегда будем получать спин вправо и не заметим никакой суперпозиции. Таким образом, наличие/отсутствие суперпозиции зависит от выбора координатных осей, то есть от базиса измерения. В одном базисе суперпозиция есть, в другом — нет.
Таким образом, если мы возьмём другой базис, например, |p⟩ и |m⟩, то при измерении собственно векторов |p⟩ и |m⟩ мы всегда будем получать однозначный результат, а состояние 0 теперь уже будет выглядеть, наоборот, как суперпозиция: |0⟩ = 1/√2*|p⟩ + 1/√2*|m⟩ ≈ 0.71*|p⟩ + 0.71*|m⟩.
Выбор базиса зависит от того, в каком предполагаемом состоянии находится наш кубит. Если мы знаем, что он находится в p или m, но не знаем, в каком именно, то измерять его в базисе |0⟩ и |1⟩ бессмысленно. Это не даст нам никакой информации, мы всегда будем получать чисто случайный результат. А вот измерение в базисе |p⟩ и |m⟩ как раз позволит однозначно различить эти два состояния.
В простенькой интерактивной визуализации по ссылке вы можете поиграться с квантовыми измерениями, меняя состояние частицы и базис прибора.